如何理解“晶体结构”？
晶体结构=晶格+基元
晶格：是一种数学上的抽象，它是由数学上的几何点在空间有规律地作周期性的无限重复构成
基元：在晶格的每一个格点上，附有一群完全相同的原子，这样一个完全相同的原子群称为基元

什么是原胞？
是指一个晶格最小的周期性单元。
a. 对三维晶格来说可以是一个平行六面体，对二维晶格可以是一个平行四边形。
b. 原胞的选取不是唯一的。
c. 判断最小周期性单元的标准只要考察这个重复单元中是否只包含一个格点。

什么是晶格基矢？
原胞的边矢量，一般用\vec{a_1}，\vec{a_2}，\vec{a_3}表示

如何计算原胞体积?
V=\vec{a_1}\cdot(\vec{a_2}\times\vec{a_3})

简单立方晶格、面心立方晶格、体心立方晶格的原胞基矢？

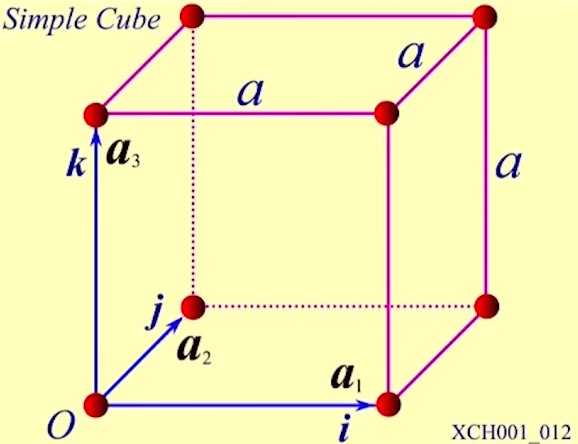
a. 简单立方晶格
基矢：\vec{a_1}=a\vec{i}，\vec{a_2}=a\vec{j}，\vec{a_3}=a\vec{k}
原胞体积：V=\vec{a_1}\cdot(\vec{a_2}\times\vec{a_3})=a^3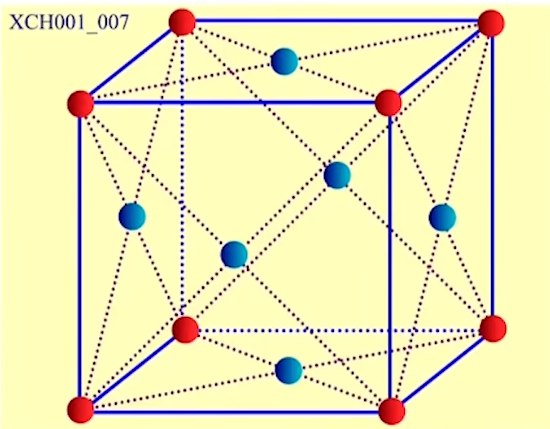

b. 面心立方晶格
基矢：\vec{a}_1=\frac{a}{2}(\vec{j}+\vec{k})，\vec{a}_2=\frac{a}{2}(\vec{k}+\vec{i})，\vec{a}_{3}=\frac{a}{2}(\vec{i}+\vec{j})
原胞体积：V=\vec{a}_1\cdot(\vec{a}_2\times\vec{a}_3)=\frac{1}{4}a^3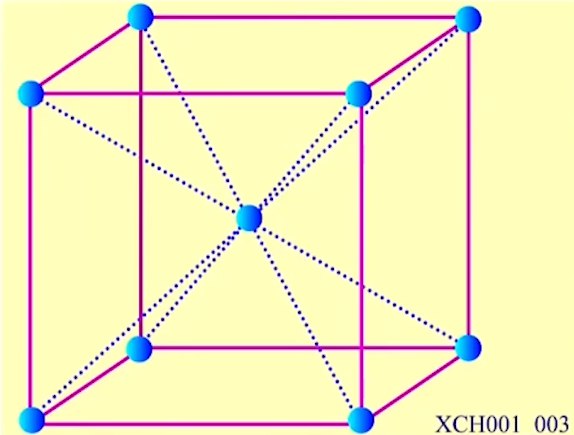

c. 体心立方晶格
基矢：\vec{a}_{1}=\frac{a}{2}(-\vec{i}+\vec{j}+\vec{k})，\vec{a}_{2}=\frac{a}{2}(\vec{i}-\vec{j}+\vec{k})，\vec{a}_{3}=\frac{a}{2}(\vec{i}+\vec{j}-\vec{k})
原胞体积：V=\vec{a}_1\cdot(\vec{a}_2\times\vec{a}_3)=\frac{1}{2}a^3